Understanding the existing issues in student learning contributes to the improvement of education in general, as it helps to develop strategies to deal with problematic factors. Primarily, it refers to the methods of developing relational understanding among students. The primary evidence for such an argument is the analysis of the examination questions and the success of students in specific areas. It will help to argue the thesis and to identify which areas cause difficulties. In this regard, given today’s difficulties in understanding senior and secondary mathematics, there is a necessity to change the traditional methodology.
As it was mentioned, in order to effectively develop a strategy for changing and improving the traditional methodology, it is necessary to find the problematic aspects. Thus, one needs to identify an absence of understanding using data from the examiner’s report. It will help to find those areas that are challenging for students and, accordingly, develop the basis for an improvement strategy. According to the report, most students found questions accessible. However, there were some challenges in applying key knowledge and skills (Further Mathematics Examination Report, 2020). Questions 13, 15, 19, 26, and 30 from the Core were challenging for most part of the students. Thus, it formulates the first area of absence of understanding.
In most cases, students had no difficulty with questions that were related to the standard, routine calculations, or interpretations. However, students did not score on questions that required the use or analysis of graphical or tabular information, such as Questions 4, 15, and 19 (Further Mathematics Examination Report, 2020). Besides, it confirms the notion that the students’ mindsets and relational understanding play a key role in their math and science achievement (Dweck, 2008; Skemp, 2022). Furthermore, one faced difficulties in forming a rule for a compound interest investment (Further Mathematics Examination Report, 2020). Moreover, students did not succeed in a change in condition part way through the problem (Further Mathematics Examination Report, 2020). Thus, being aware of such data will help to identify the underpinning relational understandings or forms.
In order to develop alternative ways of developing underpinning relational understanding, it is necessary to analyze this term. Primarily, it refers to the ability to analyze notions along the continuum, implement related concepts, and develop one’s own models (Proceedings of the National Conference of Quality Teaching, 2001). In other words, underpinning comprehension is the student’s basic ability to analyze and use the information for specific tasks. After analyzing the examination report and questions, one can conclude that the first model should improve the ability to apply key knowledge and skills. Thus, it may be achieved through the logic developing underpinning forms, such as logical tasks or tests.
The second area of absence of understanding was connected with graphical or tabular information analysis. Moreover, students often complain that they find it challenging to be driven by formulae and other complex structures (Barbeau & Taylor, 2009). From this, one may conclude that the following alternative underpinning the relational understanding model may be based on visual and structural perception improvement (Watson, 2003). This should be in the form of tasks and interactive activities responsible for enabling structural and visual analysis. Thereby, such underpinning forms will help to develop in students’ aspects that, for various reasons, were not as developed as the rest. Given that the analysis of the report was based on testimonies from many people, this formulates a majority model.
Furthermore, it is essential to identify the reason why mathematics education constitutes a problem. Certainly, the primary reason lies in exam reports and the lack of alternative underpinning understanding. Besides, some authors make similar assumptions and conclusions in related literature. It includes those mentioned in the paper and some other opinions. For example, Dweck (2008) and Skemp (2022) mention underpinning relational understanding and students’ mindset models as an urgent issue. It is research literature and provides solid evidence for the argument. Besides, Barbeau & Taylor (2009) highlight the problem of formulae and structures applying issues in students. Further, Watson (2003) proposed visual and structural perception improvement activities. These are research-based works, however, with the elements of data for practicing teachers and provide strong evidence basement. All of these confirm the notion that mathematics education is an area of difficulty.
It is worth mentioning other views which were not applied in the paper; however, similarly to the previous one, they highlight the issue of mathematics education. For example, Lesh et al. (2010) proposed models to develop students’ mathematical modeling competencies. Their work belongs to research literature and formulates significant evidence confirming the argument. Similarly, the authors mentioned that nowadays, this area has many aspects to deal with. In the Proceedings of the National Conference of Quality Teaching (2001), quality teaching, research, and professional development notions were analyzed, and improvement models were proposed. It is an article for practicing teachers, which provides solid evidence highlighting the problem. As from the previous works, one may conclude that developing alternatives underpinning relational understanding and mathematics education is an urgent issue.
Considering all the above mentioned, the conceptual difficulty, namely the absence of relational understanding, includes difficulties in certain areas. Evidence for this notion is formulated by the questions and sectors in which the students could not answer the questions correctly. One might notice that the questions from the exam are related to this conceptual difficulty because they involve different areas. Besides, Lampert (2022) proposed a method of group learning when connecting students into certain groups. Thus, each student may help others to fulfill the understanding absence in that area, which one has significant underpinning understanding.
Finally, in terms of the proposed topic, it would be helpful to develop the task for students on the basis of one mentioned in the literature. Thus, the task is to find the area of the triangle where one has enough information (Williams, 2007). However, if one needs additional data, one should discuss it with a partner and present it to the class. Moreover, to use it in Victorian schools, it could be in the form of a computer task, where one has the opportunity to perform all the calculations and fulfill the area for additional information. As one may notice in Graph 1, there is a growing tendency for its implementation in education today (Tripathi, 2019). Thereby, it will help to develop the necessary underpinning understanding in students and follow modern trends.
To conclude, the development of alternative models of underpinning understanding is essential. In addition, one should focus on teaching mathematics as it is followed by some problems. Further, it is crucial to understand different approaches to teaching and patterns of development of problematic aspects of understanding in students. On the basis of the examination report, it was determined that there are difficulties with the use of basic skills and with structural elements. Moreover, many students experience discomfort when working with formulae and complex structures. Thus, alternative development models proposed include tasks and tests for logic and visual perception development.
References
Barbeau, E. J. & Taylor, P. J. (2009). Challenging mathematics in and beyond the classroom. Springer.
Dweck, C. S. (2008). Mindsets and math/science achievement. Stanford University.
Lampert, M. (2022). Teaching problems and the problems of teaching. Yale University Press.
Lesh, R., Galbraith, P., Haines, C. R., & Hurford, A. (2010). Modeling students’ mathematical modeling competencies. Springer.
Proceedings of the National Conference of Quality Teaching. (2001).
Skemp, R. R. (2022). Mathematics teaching Incorporating Micromath.
Watson, A. (2003). Mathematics education research; innovation, networking, opportunity: proceedings of the 26th annual conference of the Mathematics Education Research. MERGA Inc.
Williams, G. (2007). Deep understanding of ‘big ideas’ in mathematics” what does this ‘look like’? Mathematics: making sense of our world, 56.
Appendix A
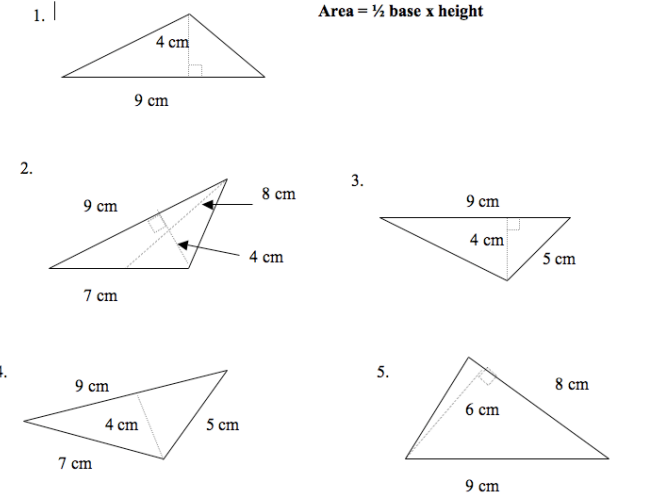
The original task from the literature. The proposed modified task was developed on the basis of this and is mentioned in the work.