Multiplication and Critical Thinking: Lesson Plan

Description

• Grade Level: 2.
• Subject: Multiplication.
• Time Required; 60 minutes.
• Materials Required: worksheets; digital interactive tools for demonstrating multiplication rules (created with the help of Google Docs); textbook.
• Key Terms:
  • Times.
  • Per.
  • Double.
  • Triple.
  • Quadruple.
  • Equal.
• Learning Objectives: introducing students to the concept of multiplication and teaching them to perform basic multiplication tasks with the easiest multipliers (e.g., 3, 4, 6); preparing students for learning the multiplication table by heart.

Introduction (5 minutes)

The teacher will ask the students about the situations in which they must count multiple objects quickly. After the students share their experiences and agree that the specified task is quite exhausting, the teacher introduces them to the concept of multiplication as the means of counting numerous objects within seconds. Visuals and, particularly, the sue of digital tools for visualizing the process of multiplication, will be utilized as the means of assisting learners in approaching the issue from a critical perspective.

Explicit Instruction (5 minutes)

At this stage, the teacher introduces learners to the concept of repeated addition. The first couple of examples are short, but afterward, the range of numbers to add increases so that the learners could recognize the necessity to substitute the repetition with a shorter way of arranging information. At this stage, the students are encouraged to critically evaluate the necessity of using multiplication in the scenarios that require repeated addition (Khasanah et al., 2018, March). Thus, students develop a strong sense of understanding of the concept at hand.

Guided Practice (10 minutes)

During the guided practice, the learners are offered a set of problems requiring using multiplication. Starting with basic ones, the problems will progress from simple tasks of multiplying small numbers, such as three times four, to simple scenarios in which students will have to define the factors and learn to determine the problem, thus, structuring it accordingly. Representing the notion of guided discovery as the method that encourages students to develop their idea of the subject matter independently, the specified framework will allow them to learn the principles of multiplication faster (Supriadi et al., 2018). Furthermore, the guided practice process will involve peer assessment, during which students will be encouraged to evaluate one another’s responses (Mariyana, 2019). The specified strategy will allow introducing options for peer learning, which will assist students in resolving the issues that they may fail to explain or communicate properly to the teacher yet can understand on a peer level.

Independent Working Time (10 minutes)

In the course of the independent practice, the students will be provided with three sets of problems. The first two will be represented solely by numerical data. Specifically, at level 1, the learners will need to transform repetitive summations into multiplications. For instance, they will need to represent “2+2+2+2” as “2∙4.” The second set of problems will include a set of multiplications for which the learners will have to provide answers (e.g., 3∙2=6). Finally, the third set will involve problems requiring the application of critical thinking. Namely, the students will be offered scenarios in which specific numbers will have to be multiplied. The students will need to determine the factors and calculate the answer to solve the task. An example of the assignment in the specified category may include a visual containing rows of objects that students will have to transform into multiplication problems and then solve them (see Fig. 1 below).

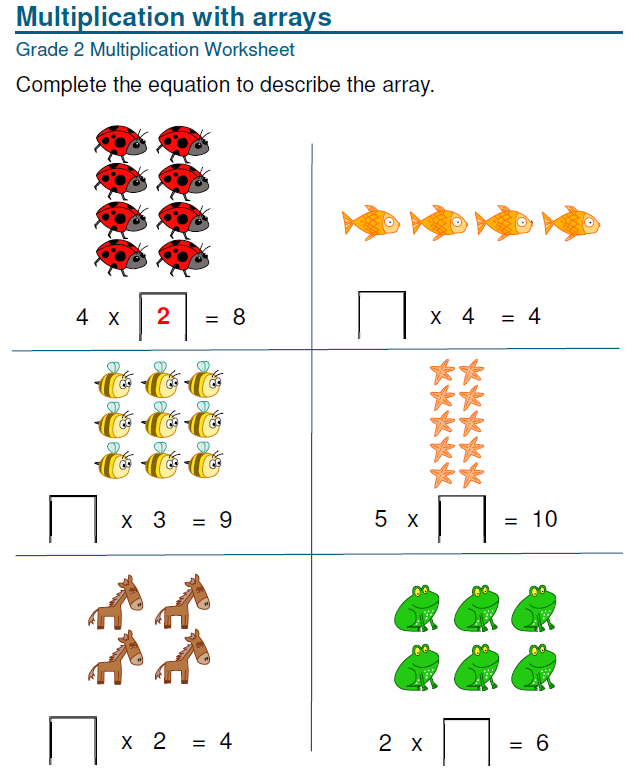
The proposed activity will encourage the students to deploy critical thinking by singling out the factors and learning to define them independently. Moreover, the exercise under analysis will introduce learners to a broader context of using critical thinking in multiplication. Namely, the activity in Part C will demonstrate the practical use of multiplication, such as the necessity to count specific objects quickly. Thus, the students will learn to analyze the situation and group objects accordingly to form a coherent multiplication framework. As a result, it is expected that the students will develop an intuitive and accurate understanding of multiplication as a notion. At the specified stage, the role of the teacher will involve observing and providing feedback at the end of the practice. As a result, the students will apply their critical faculties accordingly.

Assessment (10 minutes)

Similarly to the independent practice, the assessment will involve three key stages. Namely, the students will be provided with multiple-choice questions that will test their understanding of the subject matter. Namely, they will be suggested to select the correct definition for multiplication, select the elements of multiplication, and choose the correct statements regarding the process. Afterward, the students will be offered a set of simple tasks involving multiplying numbers. The third and the final stage will require students to solve simple problems involving visual cues, similarly to the Part C assignment in the Independent Practice section. Thus, the teacher will be able to test the learners’ understanding of the subject matter, determine the extent of their ability to apply the newly learned skills to practice, and assess their critical thinking skills by observing them transferring their newly developed understanding of multiplication to solving practical problems.

Review and Closing (20 minutes)

At the review stage, feedback regarding the students’ performance in the assessment will be provided. To ensure that all students are provided with the required support and feedback, they will be asked to state the answers to each task individually, with the correct answer being reveled in the end. Thus, the teacher will be able to control the students’ performance efficiency and identify the students that have issues with understanding the material. After each answer is revealed, one of the students will be asked to provide a detailed description of how the task was accomplished, with the teacher offering feedback. The specified stage is vital to ensure that the learners who have made mistakes could follow the logic of the solution and deploy their critical thinking faculties to understand the principal framework for multiplication.

Finally, at the closing stage, the students will be invited to reflect on how they can use multiplication in their daily life. The learners will be invited to reflect on the manner in which they are likely to apply multiplication to solving everyday tasks. Furthermore, the basis for the information to which the students will be introduced the next lesson will be developed. Namely, among the questions that the learners will be asked, the ones that will hint at the topic to be discussed during the next lesson will be incorporated into the discussion. Thus, the students will have enough information to consider after the classes (Sung et al., 2017). Finally, the learners will be provided with a home assignment and brief explanations as to how it should be completed. It is believed that the proposed format of the lesson will help the students to develop an approach toward learning that will be based on critical thinking. Specifically, the students will gain the ability to approach new topics analytically. Thus, the process of self-directed learning can be launched.

Critical Thinking: Reflection

The development of critical thinking faculties in learners is one of the vital tasks that a teacher faces, particularly, when working with young learners. In Mathematics, the opportunities for fostering critical thinking in learners are quite ample since the subject in question requires the application of critical and analytical skills (Prayogi & Yuanita, 2018). In the described context, critical thinking abilities will be developed by allowing students to approach the concept of multiplication from the perspective of its everyday use.

Additionally, the evaluation of other students’ responses and the sue of peer assessment as the elements of the lesson will allow the students to apply a well-balanced critical approach toward assessing both mathematical and social phenomena. Specifically, the analysis of the correctness of the answer will represent only one facet of the specified part of the task (Sung et al., 2017). Additionally, learners will have to connect the perspective offered by their peers to that ones that they themselves have developed in the course of the lesson. As a result, a robust and critical discussion of the issue is expected to take place in class.

Overall, the promotion of critical thinking in learners by incorporating innovative tools and the design based on peer assessment and guided discovery will allow them to build critical thinking skills rather quickly. Therefore, the suggested lesson plan is expected to boost the learners’ understanding of the subject matter. Additionally, their enthusiasm and engagement are expected to grow as a result of an increase in their agency as learners. Therefore, the use of guided discovery is expected to assist the students in their further mastering of Mathematics.

References

Khasanah, V. N., Usodo, B., & Subanti, S. (2018). Guided discovery learning in geometry learning. In Journal of Physics: Conference Series, 983(1), 1-5. Web.

Mariyana, R. (2019). The effectiveness of guided-discovery and instructional media on early mathematical skills. Indonesian Journal of Early Childhood Education Studies, 8(1), 34-37. Web.

Multiplication with arrays. (n.d.). Web.

Prayogi, S., & Yuanita, L. (2018). Critical inquiry based learning: A model of learning to promote critical thinking among prospective teachers of physic. Journal of Turkish Science Education, 15(1), 43-56. Web.

Sung, W., Ahn, J., & Black, J. B. (2017). Introducing computational thinking to young learners: Practicing computational perspectives through embodiment in mathematics education. Technology, Knowledge and Learning, 22(3), 443-463. Web.

Supriadi, N., Syazali, M., Lestari, B. D., Dewi, E. S., Utami, L. F., Mardani, L. A., & Putra, F. G. (2018). The utilization of project based learning and guided discovery learning: Effective methods to improve students’ mathematics ability. Al-Ta Lim Journal, 25(3), 261-271. Web.